Przypadkowe regularności
WYDZIAŁ MATEMATYKI I INFORMATYKI
INSTYTUT MATEMATYKI
Wyobraźmy sobie przypadkowe spotkanie szóstki ludzi. Zawsze znajdziemy wśród nich takie trzy osoby, że każda będzie znać dwie pozostałe lub trzy takie, że żadna z nich nie zna dwóch pozostałych. Dlaczego? To tylko przykład ilustrujący problemy, którymi zajmuje się grupa naukowców z Instytutu Matematyki Uniwersytetu Jagiellońskiego.
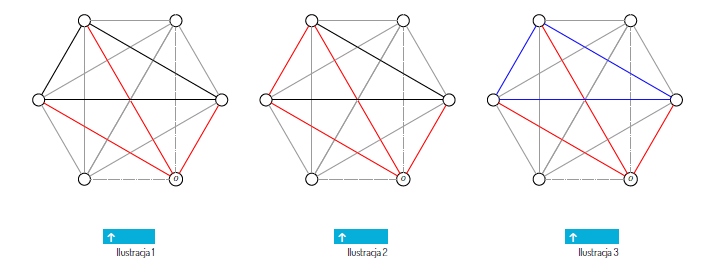
Ustawmy te sześć osób w sześciu punktach położonych na okręgu i połączmy te punkty odcinkami. Pokolorujmy odcinek na czerwono, jeżeli osoby stojące na jego końcach się znają (zakładamy że znajomości są wzajemne), a jeżeli nie, to na niebiesko. Wybierzmy teraz jeden z punktów i oznaczmy go literą O. Jest on końcem pięciu odcinków, a każdy z nich jest w jednym z dwóch kolorów. Zatem co najmniej trzy odcinki wychodzące z punktu O będą w jednym kolorze.
Przyjmijmy, że jest to kolor czerwony (gdyby był to niebieski, rozumowanie przebiegałoby identycznie, tylko role kolorów by się odwróciły). Zatem z punktu O odchodzą trzy czerwone odcinki, których końce są wierzchołkami pewnego trójkąta (zaznaczonego na ilustracji 1 pogrubioną czarną linią). Jeżeli jedna z krawędzi tego trójkąta jest w kolorze czerwonym, to wraz z dwiema krawędziami wychodzącymi z punktu O tworzy czerwony trójkąt. Znaleźliśmy w ten sposób trójkę osób, które się nawzajem znają (ilustracja 2).
W przeciwnym razie wszystkie krawędzie naszego pogrubionego trójkąta będą niebieskie, co oznacza, że znaleźliśmy trzy osoby, z których żadna nie zna dwóch pozostałych (ilustracja 3). Dowód został zakończony. Pokazaliśmy, że nieważne jak pokolorujemy piętnaście odcinków łączących sześć punktów przy użyciu dwóch kolorów – i tak na rysunku pojawi się jednokolorowy trójkąt.
Między strukturą a chaosem
Ta prosta obserwacja to dopiero początek głębokiej matematycznej teorii nazwanej – na cześć jej odkrywcy – teorią Ramseya. Wyniki należące do tego działu matematyki mówią, że w przyrodzie niemożliwy jest całkowity nieporządek: każda dostatecznie duża struktura (nawet utworzona w sposób losowy) musi zawierać pewną regularną podstrukturę. Teoria Ramseya zajmuje się opisem takich struktur oraz próbą oszacowania, jak duże muszą one być, aby pojawiła się ciekawa podstruktura.
Jednym ze sposobów na prowadzenie tych badań jest użycie teorii ergodycznej, co zaproponował izraelski matematyk Hillel Furstenberg. Aby przybliżyć jego pomysł, musimy wyjaśnić, czym jest „układ dynamiczny". Otóż jest to matematyczny model zjawiska zmieniającego się w czasie lub przestrzeni. Nauki przyrodnicze i społeczne używają języka matematyki, aby otrzymać modele, czyli przybliżone opisy zjawisk zachodzących w otaczającym nas świecie. Ich analizą zajmuje się teoria układów dynamicznych, której twierdzenia mają pomóc w zrozumieniu i przewidywaniu ewolucji procesów opisanych przy pomocy funkcji i równań. Używamy w tym celu narzędzi pochodzących z różnych działów matematyki, czego skutkiem jest wewnętrzny podział teorii układów dynamicznych na węższe specjalizacje. Jedną z nich jest teoria ergodyczna. Bada ona ewolucję układów dynamicznych, w których da się wyznaczyć prawdopodobieństwa obserwowanych podczas niej zdarzeń. Dział ten zapoczątkował francuski matematyk Henri Poincaré, który zajmował się stabilnością Układu Słonecznego, czyli problemem odporności ruchu planet na niewielkie zaburzenia (brak stabilności może oznaczać, że przelot komety mógłby wyrzucić Ziemię z jej orbity).
Poincaré nie rozwiązał problemu stabilności, ale zmagając się z nim, udowodnił twierdzenie o powracaniu. Dotyczy ono układów, w których prawdopodobieństwo zaobserwowania zdarzeń nie zmienia się w czasie. Dla takich układów każde zdarzenie, które może wystąpić raz, musi powtórzyć się nieskończenie wiele razy. Pomysł Furstenberga polegał na powiązaniu ramseyowskiego fenomenu pojawiania się regularnych podstruktur w dostatecznie dużych strukturach losowych z powracaniem (w sensie Poincarégo) pewnych konfiguracji w odpowiednio dobranych układach dynamicznych.
Pierwszym sukcesem metody Furstenberga był nowy dowód twierdzenia Szemerédiego. Samo twierdzenie dotyczy regularności występujących w dostatecznie dużych podzbiorach zbioru liczb naturalnych. Jego wypowiedź jest zbyt techniczna, aby ją tu przytoczyć.
Możemy jednak przedstawić twierdzenie van der Waerdena, które jest prototypem twierdzenia Szemerédiego. Wyobraźmy sobie, że każdej liczbie naturalnej przypisano jeden z dwóch kolorów. Twierdzenie van der Waerdena gwarantuje, że niezależnie od tego, jak to zrobimy, dla każdej liczby naturalnej k zawsze znajdziemy jednokolorowy ciąg arytmetyczny długości k, czyli takich k liczb w jednym kolorze, że odstęp pomiędzy kolejnymi dwiema z nich jest stały (na przykład zawsze znajdziemy jednokolorowy ciąg złożony z 1320 liczb ustawionych w równych odstępach). Czytelnik może sam sprawdzić, że niezależnie od tego, jak pokolorujemy liczby 1, 2, ..., 8, 9 przy użyciu dwóch kolorów, zawsze znajdziemy jednokolorowy ciąg arytmetyczny długości 3.
Zastosowanie metod ergodycznych do problemów rozważanych w teorii Ramseya stało się początkiem ergodycznej teorii Ramseya. Dzięki nim angielski matematyk Ben Green oraz Australijczyk Terrence Tao udowodnili, że także zbiór liczb pierwszych (czyli takich, które mają dokładnie dwa dzielniki: jedynkę i samą siebie) zawiera dowolnie długie skończone ciągi arytmetyczne. Odkrycie to przyczyniło się do przyznania Tao medalu Fieldsa, najbardziej prestiżowego wyróżnienia świata matematycznego, porównywanego czasem z Nagrodą Nobla. Medal ten jest przyznawany raz na cztery lata i mogą go otrzymać tylko matematycy, którzy nie ukończyli czterdziestu lat.
Badania nad liczbami pierwszymi mają bardzo długą tradycję, a niedawno zyskały także znaczenie praktyczne ze względu na wykorzystanie liczb pierwszych w kryptografii. Ergodyczna teoria Ramseya cieszy się obecnie dużym zainteresowaniem i ciągle formułowane są dzięki niej nowe, często zaskakujące twierdzenia.
Teoria ergodyczna w Krakowie
Do niedawna na Uniwersytecie Jagiellońskim nie prowadzono badań nad tymi zagadnieniami. Wsparcie Wydziału Matematyki i Informatyki UJ oraz uzyskanie finansowania umożliwiło powstanie nowego zespołu zajmującego się między innymi ergodyczną teorią Ramseya i jej związkami z teorią układów dynamicznych, teorią liczb, kombinatoryką oraz algebrą. W jego skład weszli młodzi matematycy pracujący dotychczas w różnych działach matematyki.
Jednym z problemów, którymi będzie zajmował się zespół, jest próba opisania chaotycznego zachowania orbit, czyli trajektorii, wzdłuż których poruszają się obiekty w układach dynamicznych. W ciągu ostatnich czterdziestu lat zaproponowano wiele definicji chaosu, lecz żadna z nich nie zyskała powszechnej akceptacji. Niedawno sformułowano nową definicję chaosu w języku teorii ergodycznej. Okazała się ona przydatna przy badaniu kombinatorycznych własności orbit w układach, w których entropia, czyli pewna miara skomplikowania struktury układu jest dodatnia. Jej wprowadzenie pozwoliło na postawienie wielu interesujących pytań, które stały się punktem wyjścia prac zespołu matematyków z UJ.

